Lineaarne sõltuvus y = ax + b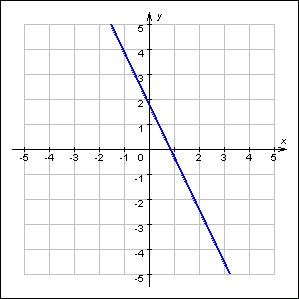

Koeffitsienti a nimetatakse sirge tõusuks. Kui a>0, y kasvax x kasvades ja sirge "tõuseb", kui a<0 "langeb" (joonisel), b on funktsiooni väärtus

kui x = 0 ja graafikult loetav kui y-telje telglõik.

Sirge tõusu arvutatakse kui: a = (Δy / Δx) sirge suvalises vahemikus.

Kui mingi muutuja kasvab lineaarselt, siis öeldakse et ta kasvab aritmeetilises progressioonis.

Aritmeetiline jada ehk aritmeetiline progressioon on jada, milles iga liikme (v.a esimese liikme) ja sellele eelneva liikme vahe on konstantne. Seda konstanti nimetatakse aritmeetilise jada vaheks. Aritmeetilise jada üldliige avaldub kujul

a_n = a₀ + nd

kus a₀ on aritmeetilise jada esimene element ehk algliige, d on aritmeetilise jada vahe ja n = 0,1,2,... (võrrelge: y = ax+b)

 

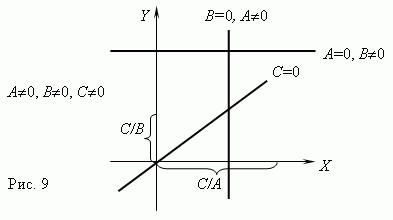
Vasakpoolsel joonisel on lineaarse sõltuvuse Ax + By = C erandjuhtumid.

Kui A = 0 iga x'i väärtuse korral y = C/B, ehk sirge on paralleelne x-teljega.

Kui B = 0 iga y'i väärtuse korral x = C/A, ehk sirge on paralleelne y-teljega.

Kui C = 0 sirge läbib koordinaatite alguspunkti.

 

 

 

 

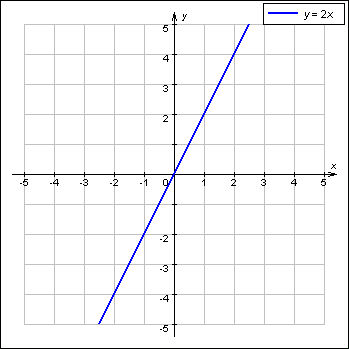
Võrdeline, ehk proportsionaalne sõltuvus y = ax

on lineaarne sõltuvus, kus b = 0 ja sirge läbib koordinaatide alguspunkti (0,0).

Sirge tõus sellisel juhul on a = y / x

Võrdelise sõltuvuse puhul kehtib võrre a = y₁/y₂ = x₁/x₂

Kui suurused on võrdelised, siis mitu korda muutub üks suurus sama palju kordi muutub ka teine suurus.

Näiteks, teate, et läbitud teepikkus ja sõidukiirus on võrdelised (S = vt, kui S₀ = 0). Kui kiirus on 2 korda suurem, siis ka sama ajaga läbitud vahemaa on 2 korda suurem. Kui teepikkust arvutame valemiga S = S₀ +vt ja S₀ ≠ 0, siis kahekordne kiiruse kasv ei kahekordista läbitud vahemaad.

 

 

 

 

 

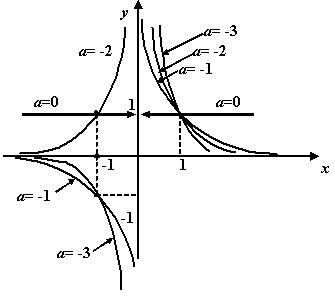
Pöördvõrdeline sõltuvus, ehk hüperbool y = a / x = ax^-1

a - on suvaline nullist erinev konstant.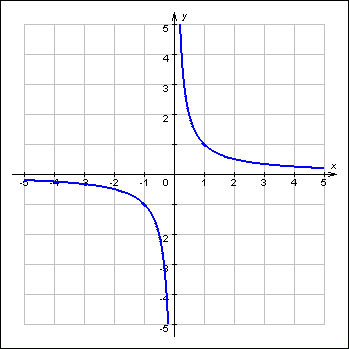

Kui parameeter a on positiivne, siis asub hüperbool koordinaatteljestiku I ja III veerandis, aga kui negatiivne, siis II ja IV veerandis.

Kahel hüperboolil ei ole ühiseid punkte (kui nad just ei ühti). Kui kujutada samal graafikul mitut hüperbooli, siis mida väiksem on a absoluutväärtus, seda lähemal asub hüperbool koordinaattelgedele.

Pöördvõrdelises sõltuvuses on omavahel, näiteks, kiirus ja aeg (v = S/t), elektrivooli tugevus ja juhi takistus (Ohmi seadus I = U/R), gaasi rõhk ja ruumala kinnises nõus ( pV = nRT).

 

 

 

 

 

 

 

 

Ruutfunktsioon y = ax²+bx+c

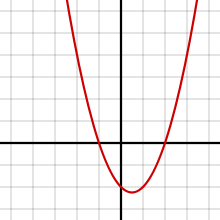
Ruutfunktsiooni graafik on parabool mis on sümmetriline vertikaaltelje suhtes.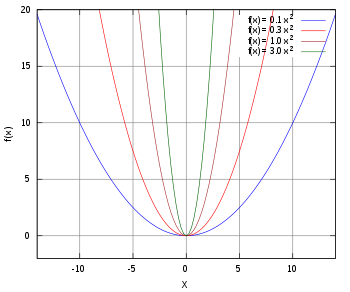

Kui a > 0, siis avaneb parabool ülespoole, kui a < 0, allapoole.

Haripunkti koordinaatdid on x = -b/(2a), y = c-b²/(4a).

Kõige lihtsamal kujul (kui b = c = 0) ruutfunktsiooni võrrand on y = ax², parabooli haripunkt asub koordinaatide alguspunktis (0,0), ning parabool on seda "kitsam" mida suurem on a väärtus (parempoolne joonis).

Paraboolpinnaga peeglid kontsentreerivad valgust mikroskoopides

ja teleskoopides. Põrkava palli, Maale lähenevate komeetide, nurga all visatud

kehade või purskaevuvee trajektoorid on paraboolid.

 

 

 

Astmefunktsioon y = x ^a

Astmefunktsiooni kuju sõltub astmenäitaja a märgist ja väärtusest. Ülalpool mainitud funktsioonid on kõik astmefunktsiooni erandjuhtumid.

Kui a = 1, funktsioon on y = x ja graafik - sirge läbi 0-punkti;

 

 

 

 

 

 

 

 

 

 

 

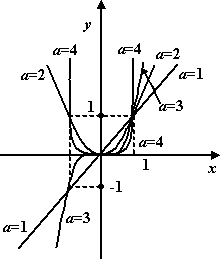
kui a on positiivne ja paarisarv, funktsioon on, näiteks, y = x² või y = x⁴ ja graafik on sümmeetriline y-telje suhtes;

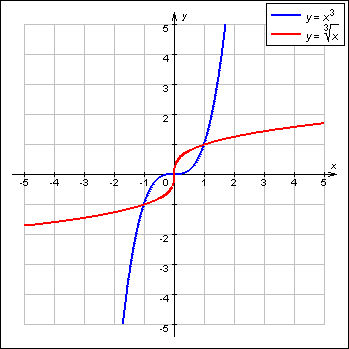
kui a on positiivne ja paaritu arv, funktsioon on, näiteks, y = x³ või y = x⁵ ja funktsiooni graafik on sümmeetriline koordinaatide alguspunkti (0; 0) suhtes;

kui a < 0 tegemist on hüperboolidega y = x^-1 või y = x^-3;

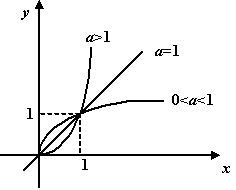
ja kui 0 < a< 1 funktsioon on kujul y = x^1/2 (ruutjuur) või y = x^1/3 (kuupjuur) ja graafikud on sümmeetrilised vastavate funktsioonide y = x² ja y = x³ graafikutega telje y = x suhtes.

Kõik astmefunktsioonid y = x^a läbivad koordinaate (1, 1) ja/või (-1,1), (-1,-1), (1,-1) sõltuvalt a ja x väärtusest.

Eksponentfunktsioon y = a^x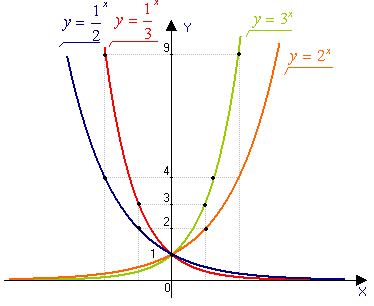

Pange tähele: a>0 . Kui a oleks negatiivne, graafik ei saaks olla pidev joon.

Näiteks, (-2)² = 4 ja järgmine punkt (-2)³ = -8, järgmine (-2)⁴ = 16 jne.

Pange tähele: kõik funktsioonid kujul y = a^x läbivad koordinaati (0,1).

Geomeetriline jada ehk geomeetriline progressioon on jada, milles iga liikme ja sellele eelneva liikme jagatis on konstantne. Seda konstanti nimetatakse selle geomeetrilise jada teguriks. Geomeetrilise jada üldliige avaldub kujul

a_n = a₀ qⁿ

kus a₀ on jada esimene liige ehk algliige ja q on selle geomeetrilise jada tegur.

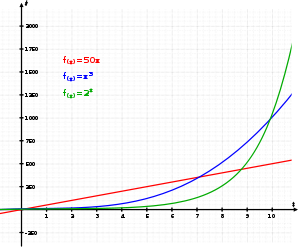
Geomeetrilises progressioonis, ehk eksponentsiaalselt kasvab inimeste arv Maakeral, bakterite arv koloonias, haigestunute arv epideemia korral , investorite arv ja kasumi suurus finantsilises püramiid-skeemis (kuni piirangute tekkimiseni), lõhustunud aatomituumade arv ahelreaktsioonis jne.

Nagu selgub vasakpoolsest joonisest, lõpptulemusena eksponentsiaalne areng on alati

kiirem kui lineaarne või astmeline.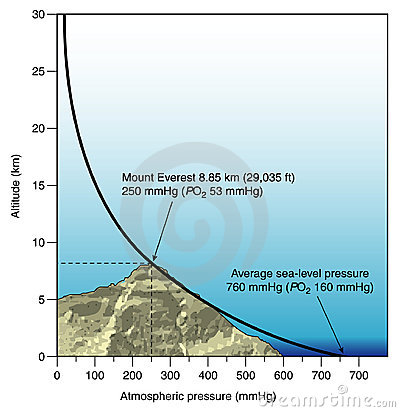

 

Eksponentsiaalselt kahanevalt, ehk geomeetrilises regressioonis toimuvad paljud looduslikud protsessid: näiteks, keha jahtumine (keha temperatuuri lähenemine keskkonna temperatuurile), kiirguse intensiivsuse nõrgenemine keskkonnas, nn radioaktiivne lagunemine (iseeneselik aatomituumade lagunemine), õhurõhu ja õhutiheduse vähenemine kõrgusega merepinnast jne.

Pange tähele: nii nagu funktsioon y = a^-x parempoolsel joonisel väga aeglaselt läheneb x-teljele, nii ka ülalnimetatud parameetrid alguses kahanevad kiiresti ja seejarel väga aeglaselt lähevad nullile.

Näiteks, vt. joonisel õhurõhu sõltuvust kõrgusest merepinnast. Umbes 5.5 km kõrgusel õhurõhk on vähenenud 2 korda, kuid ei 15 ega 30 km kõrgusel ta ei ole võrdne nulliga. Ka 50 km kõrgusel õhurõhk on üks tuhandik õhurõhust merepinnal.

 

Kõige tuntum eksponentfunktsiooni alus on nn Euleri arv e = 2.718281828.. ja funktsioon ise kujul y = e^x või y = e^-x.

Erilisus teiste hulgas seisneb selles, et funktsiooni tuletise väärtus võrdub funktsiooni väärtusega: y' = y = e^x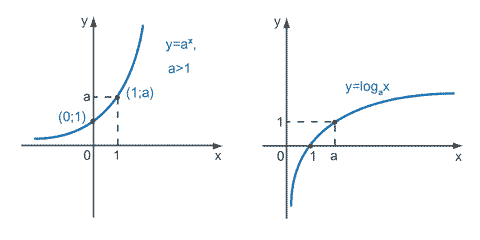

Ekponentfunktsiooni pöördfunktsiooniks on logaritm.

 

 

 

 

 

 

 

 

 

Logaritm

Kui Teil on astmefunktsioon b = a^x, siis log_a b näitab mis astmes peaks olema arv a, et tulemus võrduks arvuga b, ehk log_a b = x.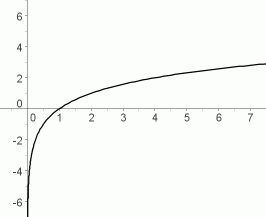

Aluse a väärtus peab olema kas 0 < a < 1 või a > 1; tavaliselt kasutatakse alustena arve 10, e või 2. Logaritmi alusel e nimetatakse naturaallogaritmiks.

 

Logaritmi omadused, logaritm korrutisest ja jagatisest, logaritm astmest:

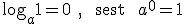
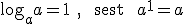
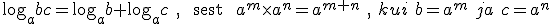
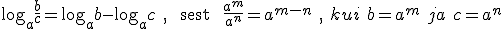
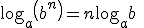
Teie kalkulaatoritel on klahvid ln x ja log x mille abil saab võtta naturaal- ja kümnendlogaritmi.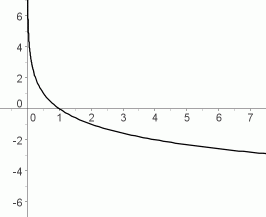

Mida teha, kui on vaja võtta logaritmi teistel alustel? Pidage meeles väga olulist logaritmi omadust:

Näiteks, kui on vaja võtta  log₂ 3, arvutage teda kui naturaal- või kümnendlogaritmide suhet:

 

 

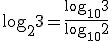
log_a x, kui 1<a<1

exp ja log funktsioonide kuju sõltuvalt parameetrite väärtusest saab jälgida aadressil:

http://mathdemos.org/mathdemos/family_of_functions/explog_gallery.html

Valige Gif Animation, peale väikest pausi jälgige funktsiooni kuju muutumist ühe või teise parameetri muutumisega. Animatsioon kordub kuni Te ei vali uut akent.

Logaritmi praktilisi rakendusi.

Logaritm-funktsiooniga Te puutute kokku oma edaspidises töös üllatavalt sageli:

- kui graafikule on vaja kanda väga laias piirkonnas muutuvat funktsiooni või argumenti, kasutatakse logaritmilist skaalat, kus muutujate asemel telgedel on nende logaritmid;

- teate, et lahuse happelisust iseloomustatake suurusega pH. pH on negatiivne logaritm lahuse vesinikioonide kontsentratsioonist (mol/l), pH = - log₁₀ [H⁺];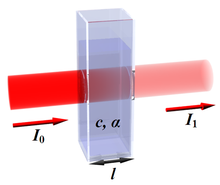

- spektroskoopias valguse neeldumist keskkonnas iseloomustatakse optilise tihedusega, mis on logaritm pealelangeva ja keskkonda läbinud kiirguste suhtest,

   A = log₁₀ (I₀/I);

- Richteri skaala on logaritmiline skaala, mida kasutatakse maavärina võimsuse hindamiseks. Näiteks on 6-palline maavärin 10 korda võimsam kui 5-palline ning

   100 korda võimsam kui 4-palline maavärin;

- Detsibell on signaalide (võimsuse, voolu, pinge) suhteline logaritmiline mõõtühik. Kuna inimkõrv reageerib heliärritusele mitte lineaarselt, vaid logaritmiliselt,    kasutatakse akustikas detsibelli helivaljuse väljendamiseks